My Finance

Background: I continue the previous post of joint work with my undergraduate student Angel Piotrowski. Consider my work arXiv:1905.04603. We wrote about this in yet another post. In a GitHub/asarantsev repository we updated our code and data.

Let be the 10-year trailing averaged annual real earnings. Let be the log growth terms. We compute these for Also, let be total real returns for the same years. Then is implied dividend yield; we assume is its long-term average. We model the valuation measure as an autoregression of order 1:

where innovations are independent identically distributed, with mean zero.

As discussed before, the difference between our research and arXiv:1905.04603 is that we take December CPI data instead of January to compute inflation, and end-of-year S&P index data instead of average January close level. Also, we consider 10-year instead of 5-year trailing window for real earnings.

Original model fit: We get innovations which are IID but not quite Gaussian. See plots below. Also, the Shapiro-Wilk and Jarque-Bera tests give us The Student test for gives us so the model is not a random walk, but rather mean-reverting.

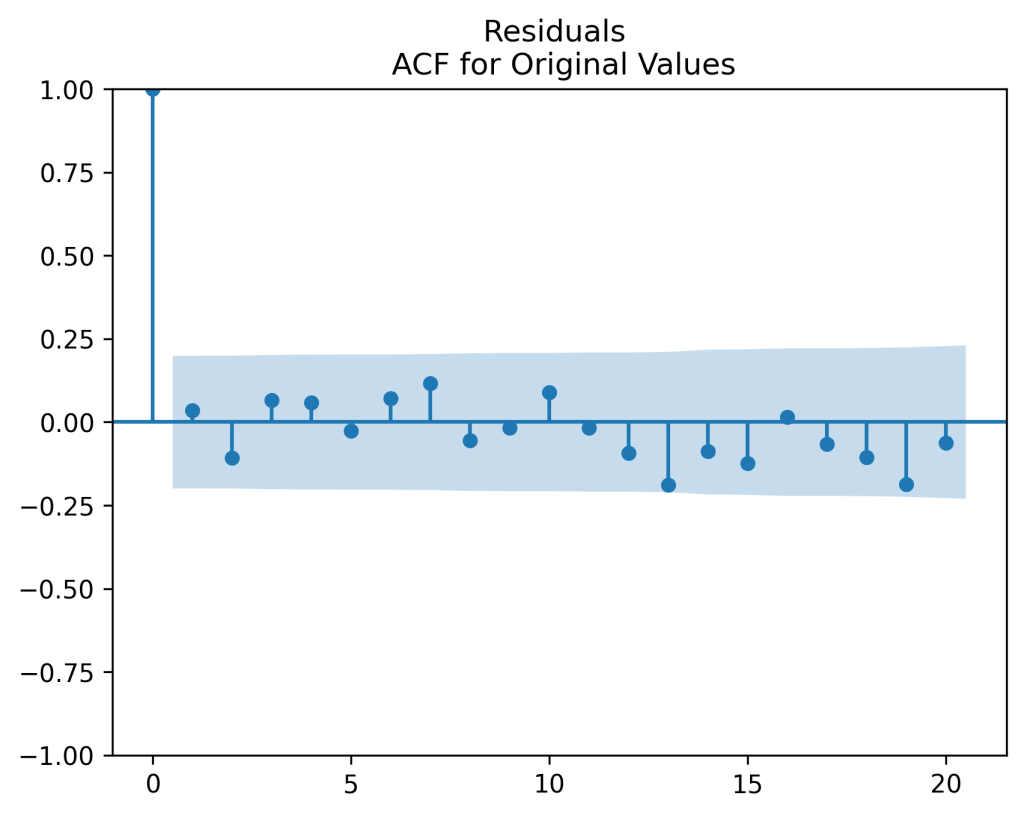
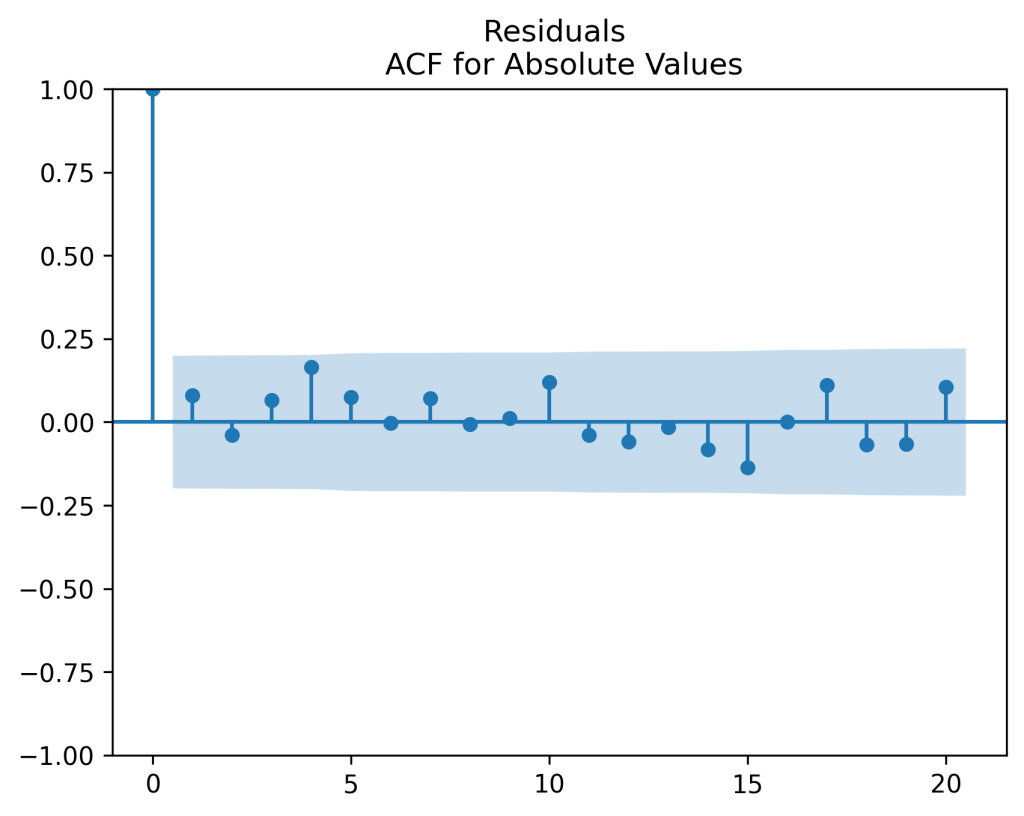
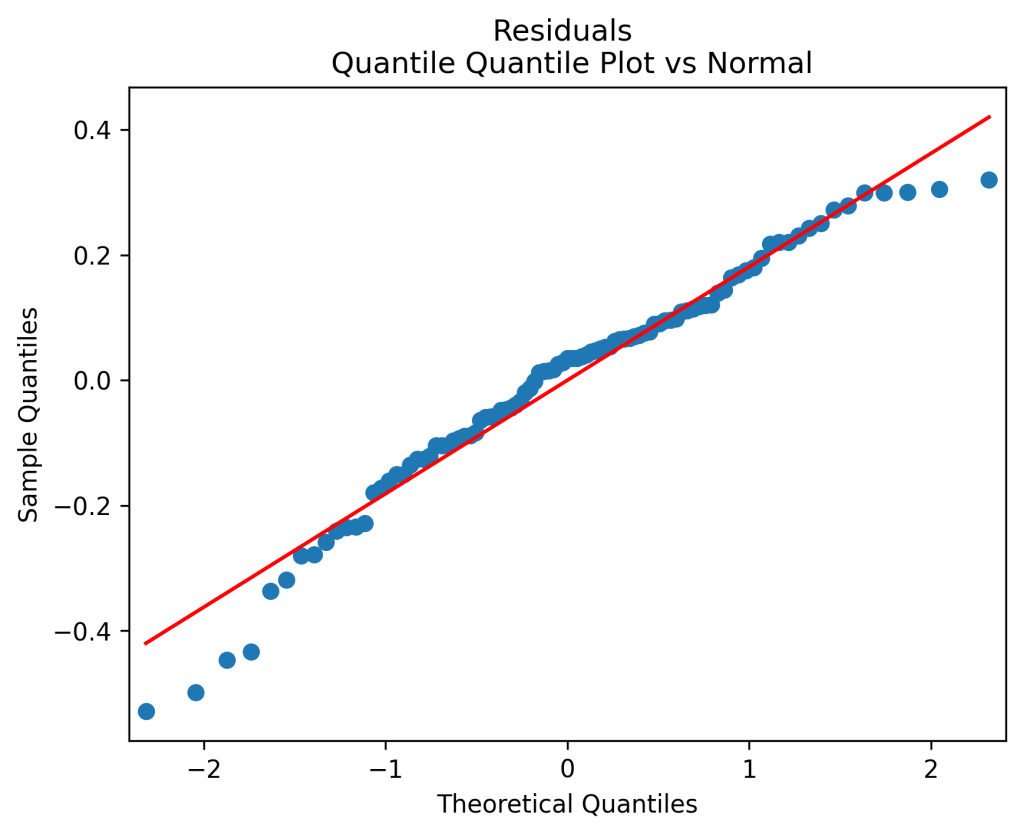
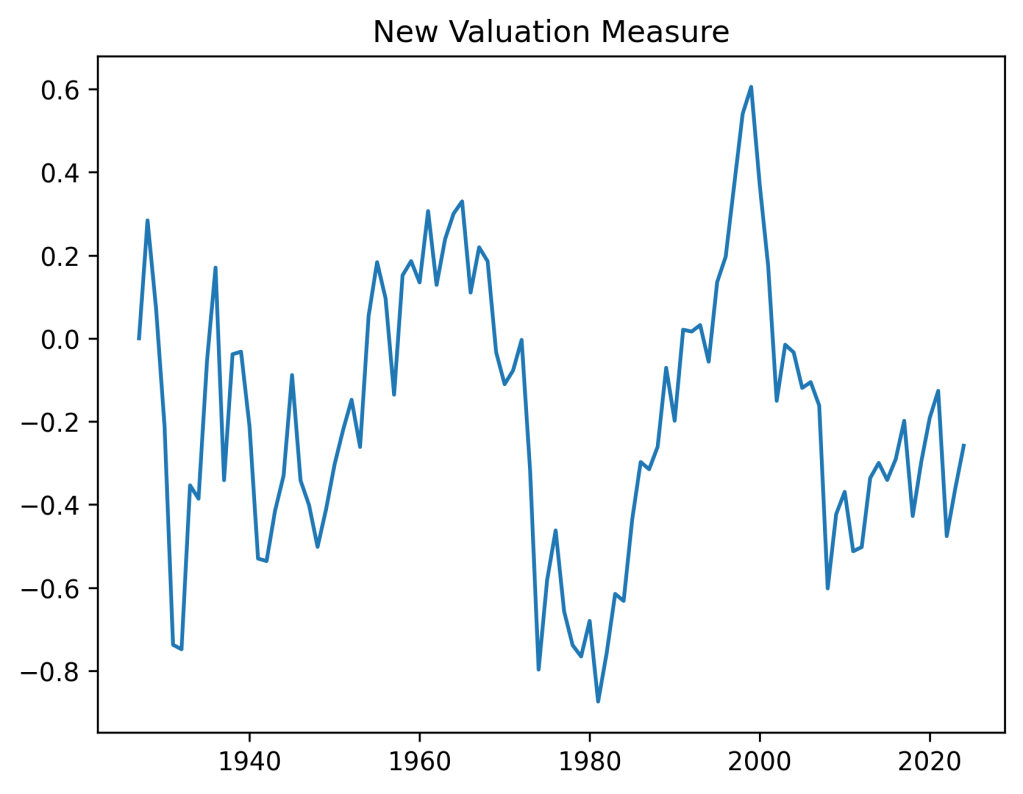
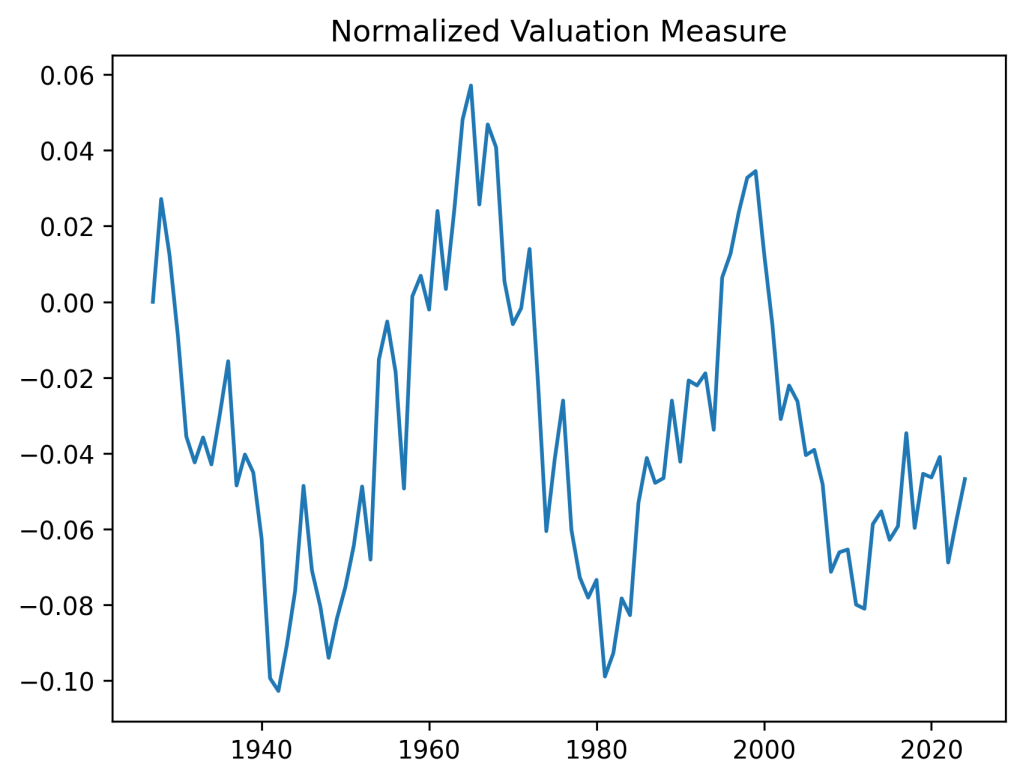
Bubbles and busts: The valuation measure has plot shown below. It is clear that the current valuation measure is well below the historical average. This is in contrast with the classic price-earnings ratio and Shiller CAPE. Both show that the S&P is currently overvalued. However, on the graph below we can see the overvaluation right before the Great Depression, in the 1960s, and at the start of the 21st century (the dotcom bubble). This graph is quite similar to the one in arXiv:1950.04603.

Normalize innovations: Next, let us divide innovations by annual volatility computed by Angel Piotrowski. The result is better: These are independent identically distributed Gaussian. Strange high autocorrelation at lag four does not change the suggestions that the innovations indeed can be modeled as IID. Shapiro-Wilk and Jarque-Bera normality tests are

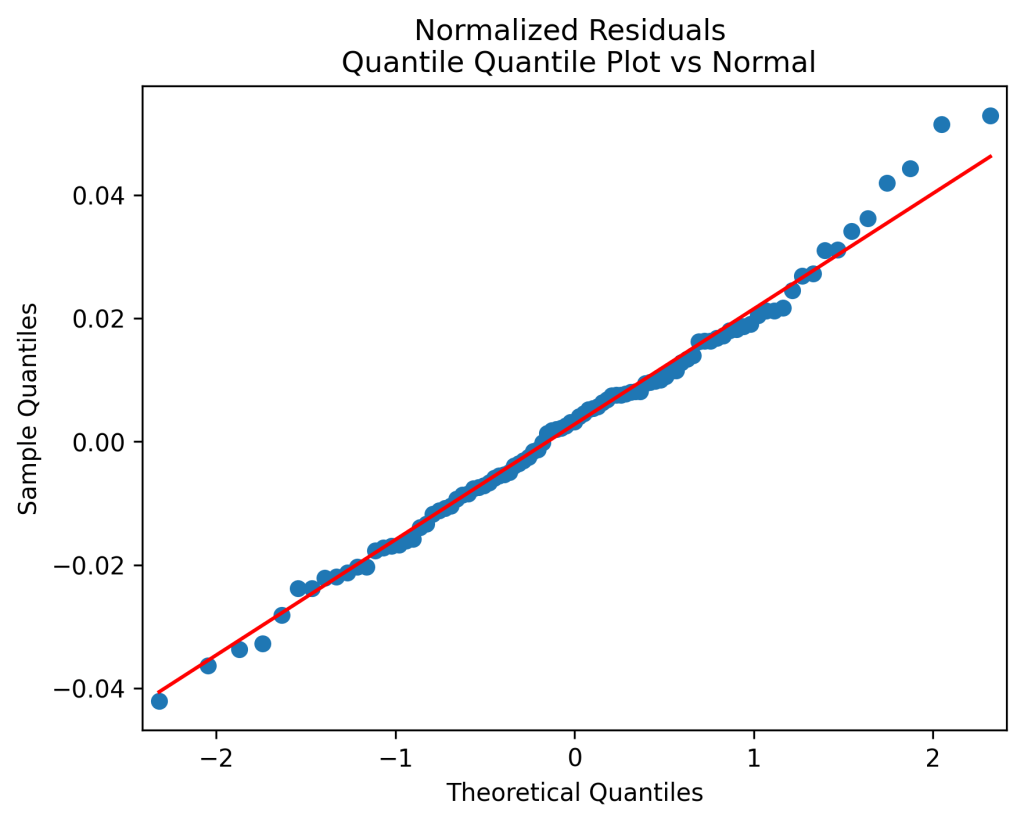
In other words, it is reasonable to model where

Normalize regression, not residuals: Alternatively, we can divide implied dividend yield by volatility and perform this autoregression for the new terms: Consider and repeat the analysis. See the plot of the valuation measure below. It looks very similar to the one above.

Again, the Student T-test gives us for Next, the Shapiro-Wilk and Jarque-Bera tests for new innovations give us The autocorrelation function plots for and for show it is reasonable to model these as independent identically distributed, and look very similarly to the above plots for instead of Further, the quantile-quantile plot for looks very similarly to the one for

The for original regression and for new regression. We leave it to the reader which one to use. But we intend to use the original regression for future financial simulator.

Update: We used the new regression in the financial simulator. We use the version without the volatility factor, which after division becomes the intercept of the ordinary least squares new regression. This makes the innovations multiplied by this volatility, but does not introduce any new factors in this model. We only compare total returns and earnings growth.