This post is continued from the previous post, which in turn continues the two posts of annual Bank of America-rated bond rates and returns. We fit the 1996-2024 data for corporate bond returns and rates.
Here, we talk about investment-grade corporate bonds in general, combining all four investment-grade ratings: AAA, AA, A, BBB. Below see the graph of these corporate bond rates, together with rates of each ratings of investment-grade bonds: AAA, AA, A, BBB. We see that investment-grade rates are closer to A or BBB, rather than AAA.
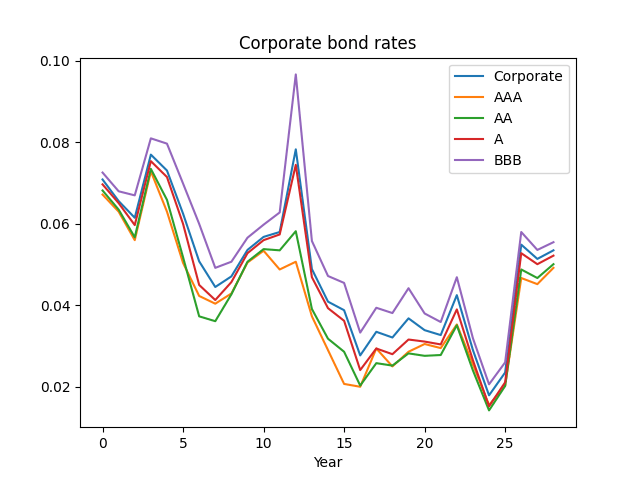
Next, plot the wealth. Then we see the same pattern. We are curious why investment-grade corporate bonds behave closer to lower-rated investment ratings, rather than AAA? Maybe there are not so many AAA rated bonds.
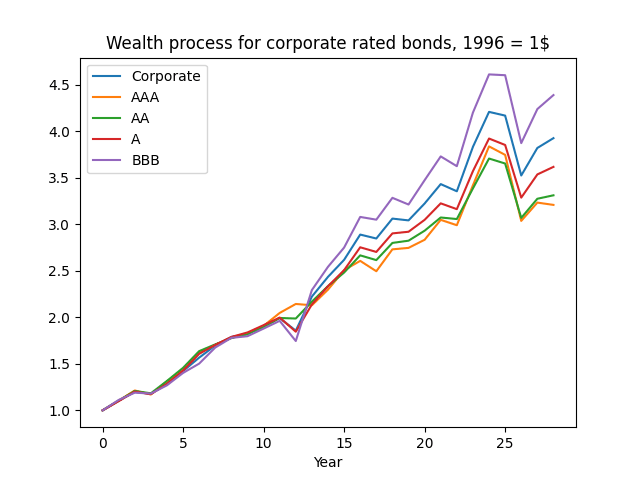
This might be the reason why in this post AAA rates do not predict corporate bond returns very well. Remember, we have data for Bank of America bond rates only from 1996 (end of year).
We have Bank of America investment-grade corporate bond returns starting from 1972. This discrepancy gives us motivation to use end-of-year weekly data for Moody’s AAA or BAA (which corresponds to BBB in Bank of America ratings) available from 1962 to predict investment-grade corporate bond returns. This gives us motivation to replace AAA with BAA Moody’s rates.
Using the cut data from 1996, we replicated results of annual Bank of America-rated bond rates and returns. The results are the same as for AAA, AA, A, or BBB. Using annual volatility makes the two regressions have IID Gaussian residuals. All is good, except the rates are available only from 1996.
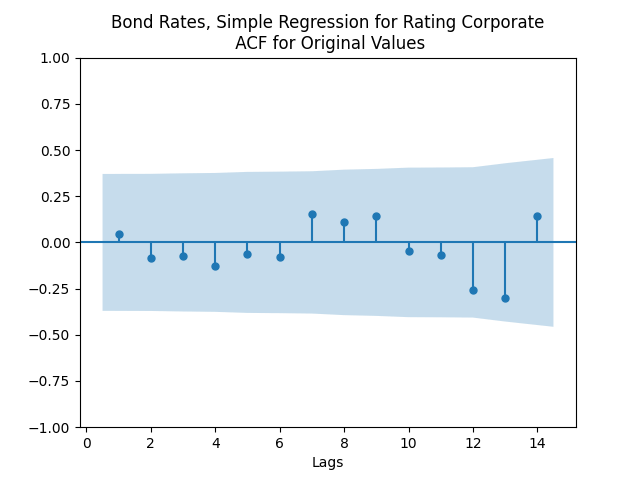
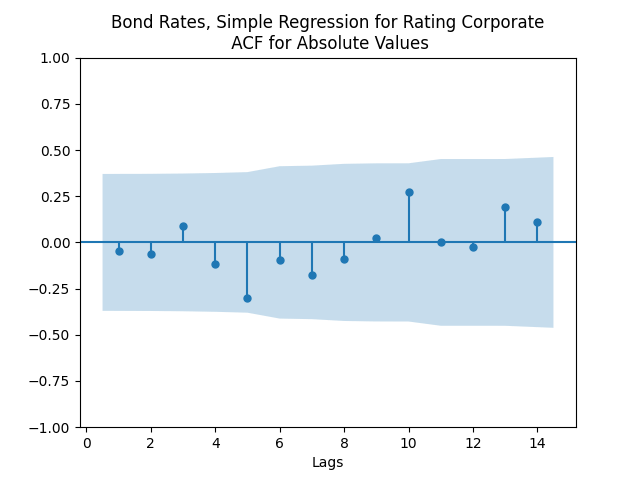
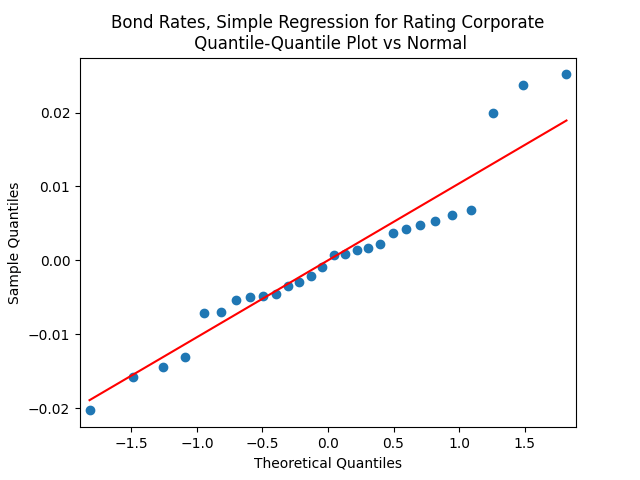
Here analysis of simple autoregression residuals for rates show they are IID but not Gaussian.
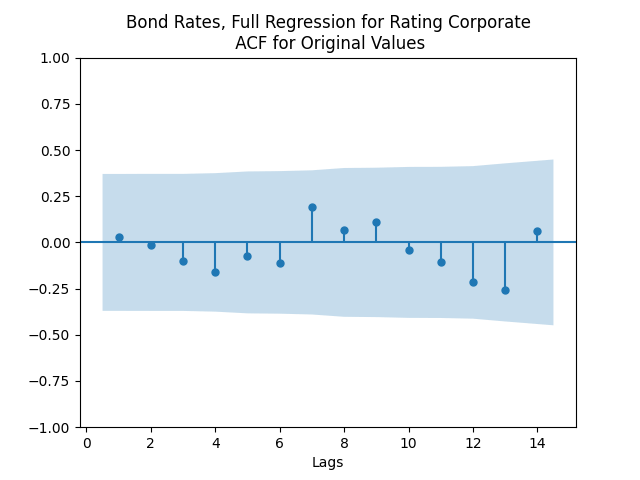
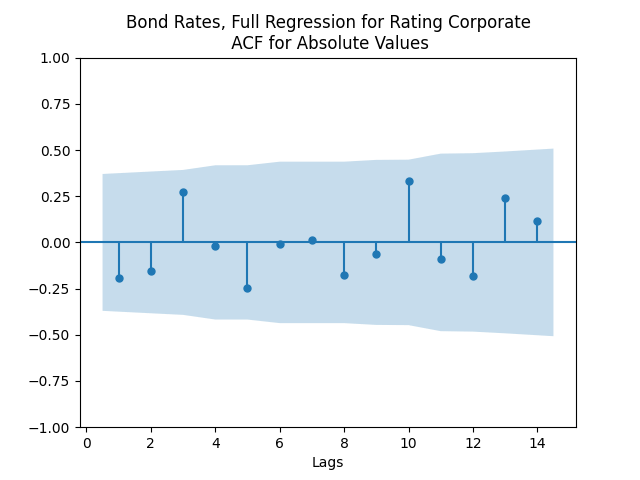
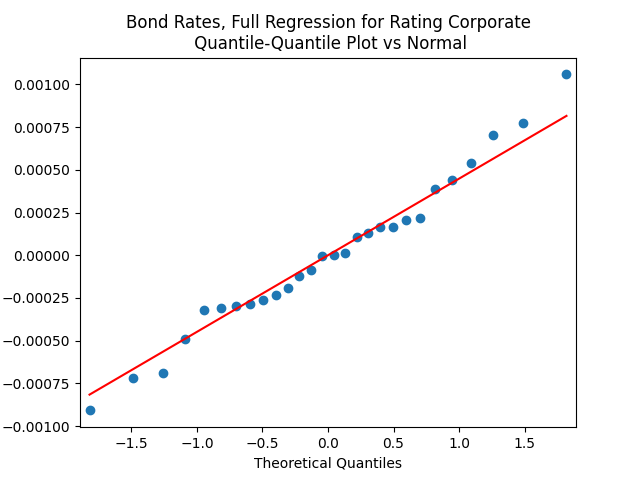
But autoregression with volatility: show these residuals are IID Gaussian. The
and coefficient estimates are
The Student T-test gives us
for
for
and
for
The Jarque-Bera and Shapiro-Wilk
The L1 values for original and absolute values of the autocorrelation function are
Model total bond returns using duration:
We see residuals below.
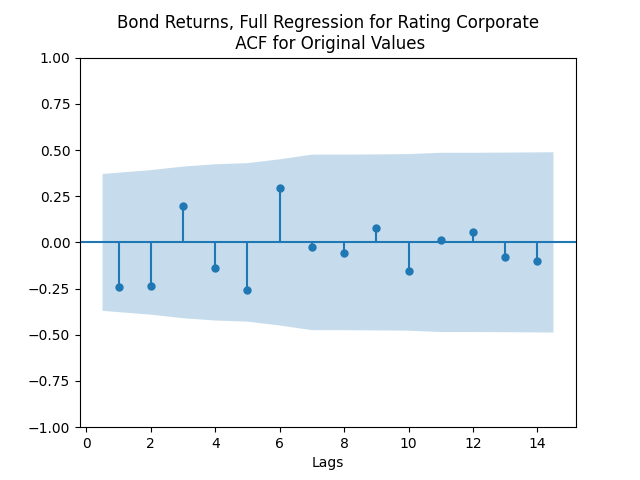
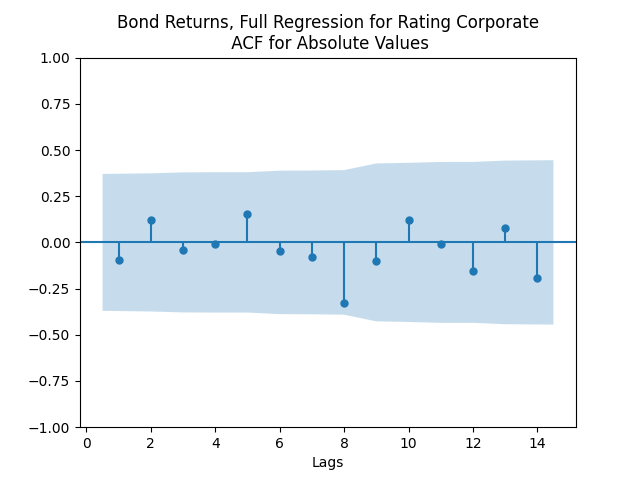
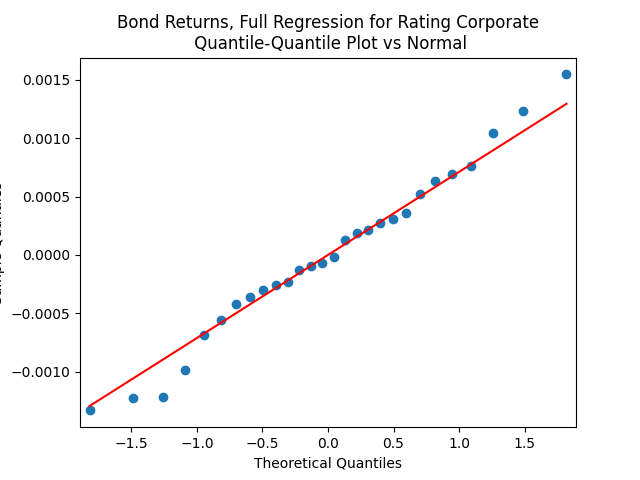
But for the simple regression without volatility we get the following residuals:
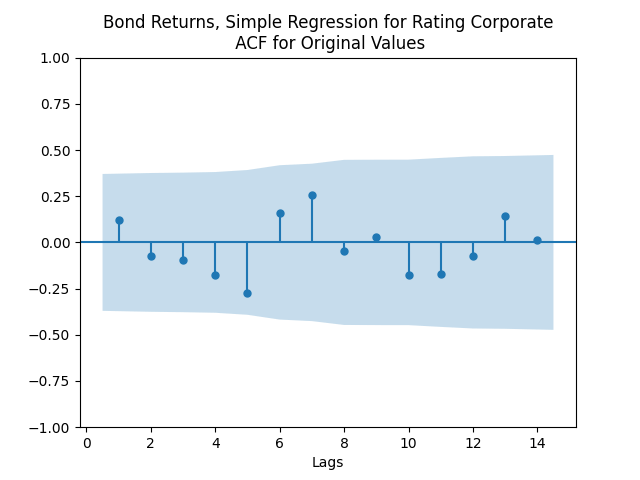
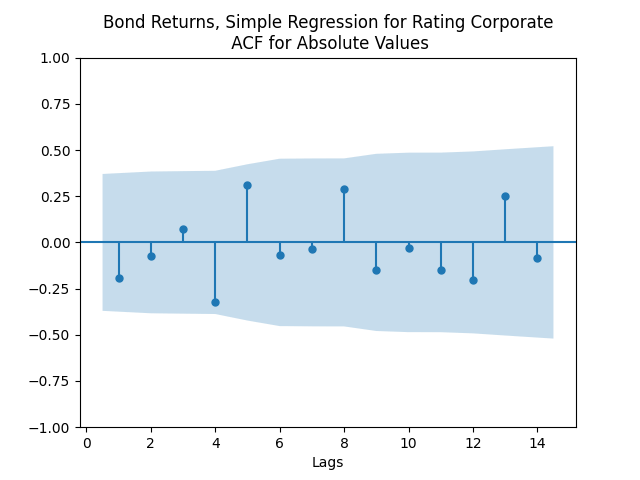
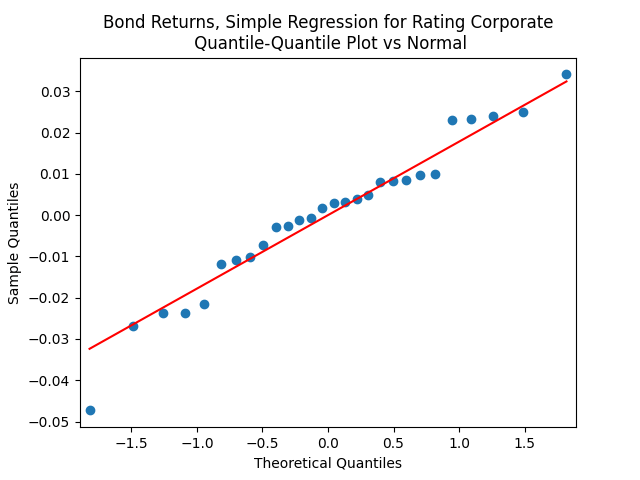
Both regressions actually have IID Gaussian residuals, judging by Shapiro-Wilk and Jarque-Bera normality tests, and the L1 values for autocorrelation function. For the simple regression, and
The value of
See the Python code and Excel data (updated) at https://github.com/asarantsev/Annual-Bank-of-America-Rated-Bond-Data
Next, let us replicate results of this blog post for BAA instead of AAA rates. We uploaded updated code to GitHub/asarantsev repository Corporate-Bonds-Annual-Data. We have data from 1972.
The simple autoregression for rates judging by the Shapiro-Wilk and Jarque-Bera tests, is better:
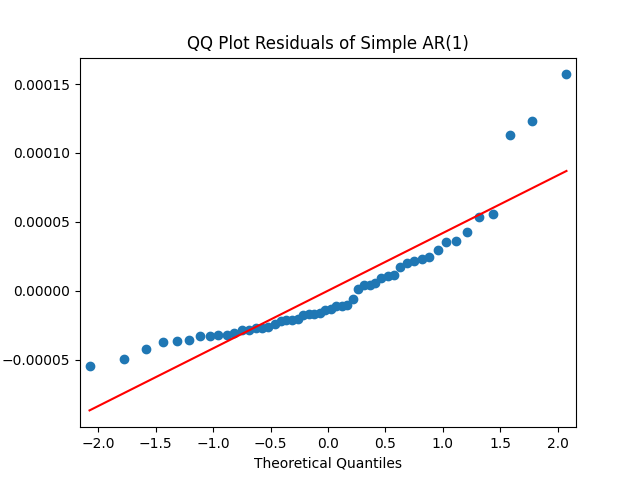
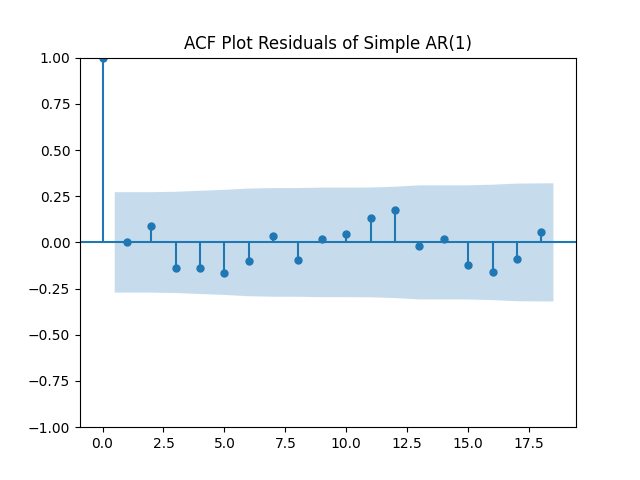
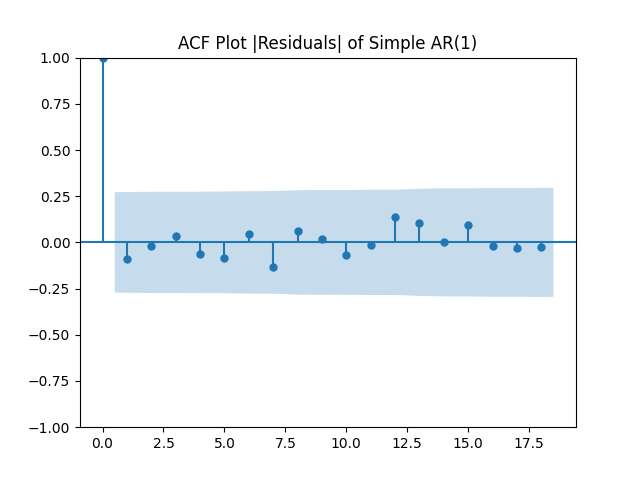
Look at residuals for autoregression for rates with volatility:
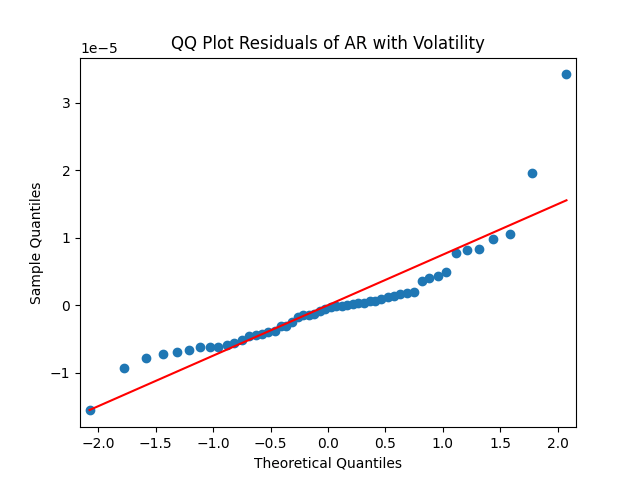
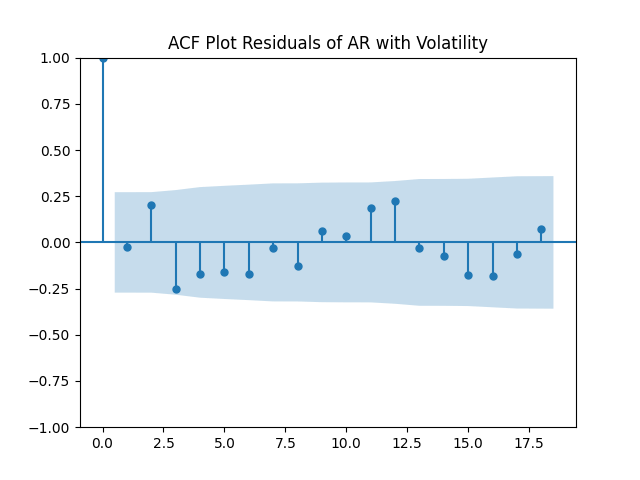
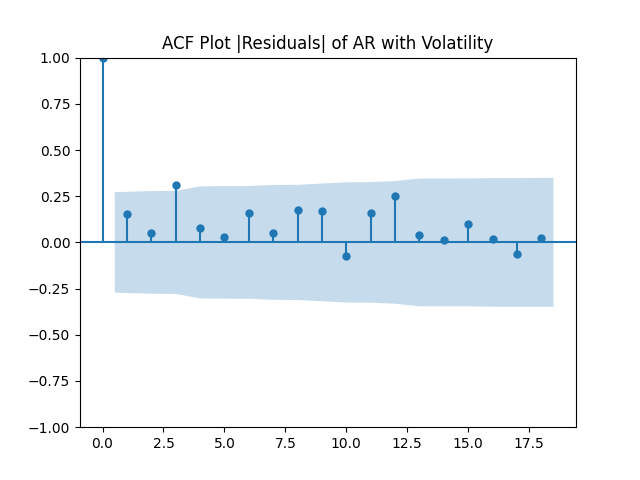
For the simple autoregression, Shapiro-Wilk and Jarque-Bera tests give us and
But for the autoregression with volatility, this gives us
and
To be fair, from the quantile-quantile plot it is hard to tell the difference. Next, for returns
minus rates
if we do not regress them upon anything but simply analyze them, surprisingly, we get the IID Gaussian.
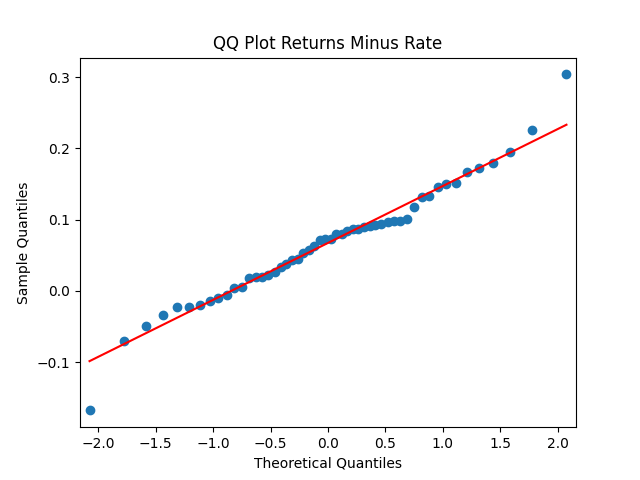
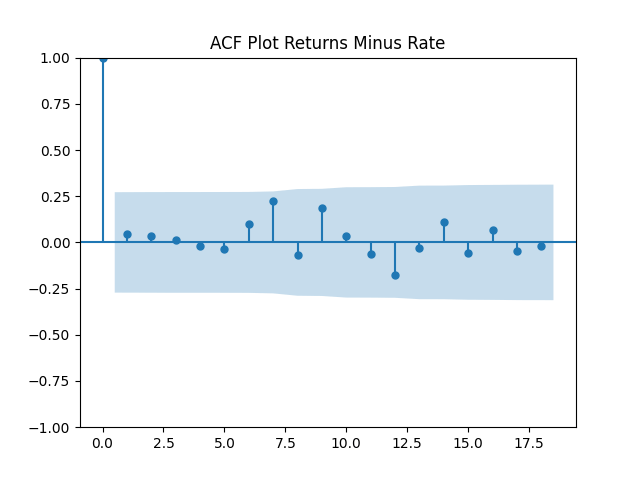

But it’s good to regress these differences upon the change in rates:
We get
where
and
And the correlation is very strong:
Of course, it is statistically significant. The Shapiro-Wilk and Jarque-Bera tests give us
Leave a reply to To Do List – My Finance Cancel reply